Bayesian Rock Paper Scissors!

So why does my JPG image of Thomas Bayes LOVE patterns?

In short, this game's algorithm uses conditional probabilities and Bayes' theorem to calculate the probability of your next move given your previous move. How can we calculate such a probability? Considering that each game generates a new piece of evidence, we can use Bayesian Inference! Let's define events E and F, where F is the probability that your next move will be rock, and E is the probability that your previous move was scissors.

Recall Bayes' Theorem:

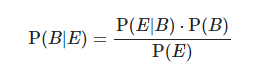
The left term represents the probability that a player plays rock given that their previous move was scissors. We expand this using Bayes', and in doing so, have established a perfect expression to which we can apply Bayesian Inference. In short, the more that a player plays, the more moves we have to go off of when calculating our probabilities. After 50 games (or more), it is only natural that we will have conditional probabilities to analyze. For example, if we want to know the probability that a player's previous move was scissors given that their current move was rock, we simply (by the definition of conditional probability) count all of the times our player picked rock after scissors, over the total amount of times they picked rock. We can call this our evidence (or observations), which would be the P(E | B) term. Our prior is also relatively simple. Before observing a person's habits and patterns of playing certain moves after others (the P(E | B) term), our initial hypothesis is simply the rate at which they have been playing rock, paper, or scissors. This is essentially the number of times this person played that specific move over the total number of moves. Without the context of these conditional probabilities, the player will have probabilities for rock, paper, and scissors, but these general probabilities do not really tell us much on their own, so they act as our priors (P(B)). P(E), or the normalization constant, is also relatively easy to track, as similar to the prior, it is just the probability of the specified move (from the player's dataset of past moves). Putting this all together, we have a pretty nifty equation in which we can track the probability of a player making any move given their previous move (a total of 9 different conditionals!). You will notice, however, after playing around with the game that some of these probabilities can have strange values (like 0). To learn why and the limitations/implementation of this approach, check out the write up! So all along, Thomas was keeping track of your patterns (Like P(Next = Rock | Previous = Scissors), P(Next = Rock | Previous = Rock), etc.). Patterns mean predictability, which means he wins! However, being the gracious mathmetician he is, he has decided to share them with you (use them wisely):